Album
Naloga
Ogrevalna naloga
Napiši program, ki izpiše
Prva vrstica programa mora biti for i in range(24):. Celoten
program (skupaj s prvo vrstico bo dolg kvečjemu štiri vrstice) naj bo
znotraj te zanke in naj ne vsebuje nobene druge zanke. Torej: program bo
imel, recimo, dva print-a in en if. Uporabljal bo eno samo spremenljivko, i.
Funkcija print gre vedno v novo vrstico; temu se izognemo tako, da dodamo poimenovani argument end, npr. print("bla bla", end="").
Obvezna naloga
Napiši program, ki pokaže vse slike v datotekah s končnico png iz trenutnega direktorija v takšni obliki:
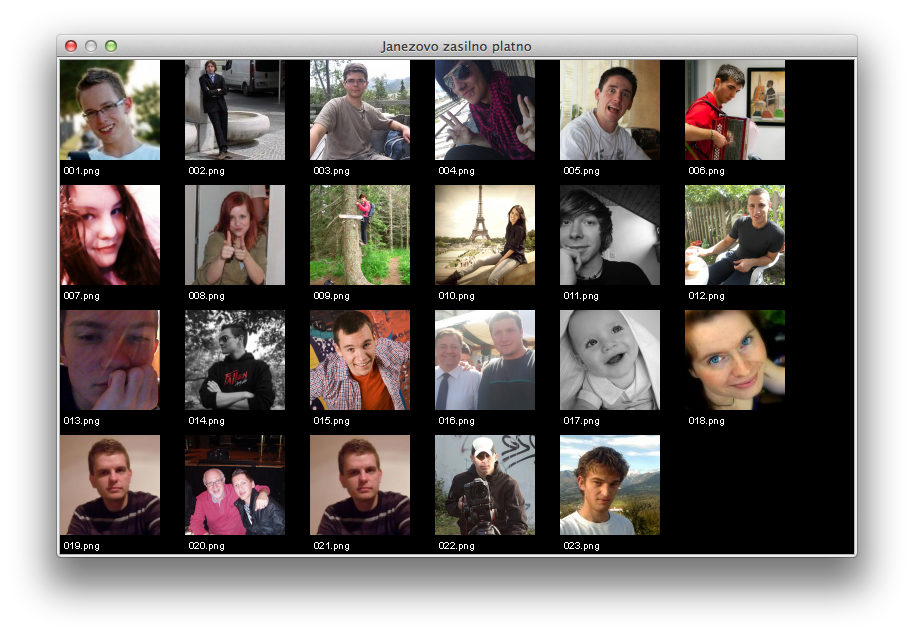
Tisto, kar si izpisoval v ogrevalni nalogi, so koordinate slik. Besedilo, to je, imena datotek, je 100 točk nižje, velikost pisave je 10.
Uporabite lahko primere slik, objavljene na Učilnici.
Pazi:
- "Brati iz trenutnega direktorija" pomeni
os.listdir("."), ne da bi prej spreminjal trenutni direktorij zos.chdirali čim podobnim. - Slike naj bodo urejene po abecedi.
- Program sme predpostavljati, da slike niso večje kot 100x100 točk;
- Program ne sme računati na to, da gre vedno za te slike ali da jih je vedno natančno 23.
- Če je slik več kot 24, naj jih pokaže le 24.
Dodatna naloga
V dodatni nalogi bo potrebno narediti kolaž slik.
Najprej napiši program, ki takole razdeli sliko.

Postopek je takšen: program (načelno) najprej prereže sliko z navpično črto. Ta je na poljubnem mestu na sliki, vendar vsaj 100 točk od levega ali desnega roba. Nastala dela reže vodoravno, pri čemer mora biti rez vsaj 100 točk od zgornjega in od spodnjega roba. Nastale dele reže navpično, te potem spet vodoravno in tako naprej. Ker mora biti rez vedno vsaj 100 točk od roba, pravokotnikov, ki so široki manj kot 200 točk, ni več mogoče rezati navpično. V tem primeru jih prerežemo vodoravno, če gre. Prav tako pravokotnikov, ki so visoki manj kot 200 točk, ne moremo rezati vodoravno, pač pa jih režemo navpično, če gre.
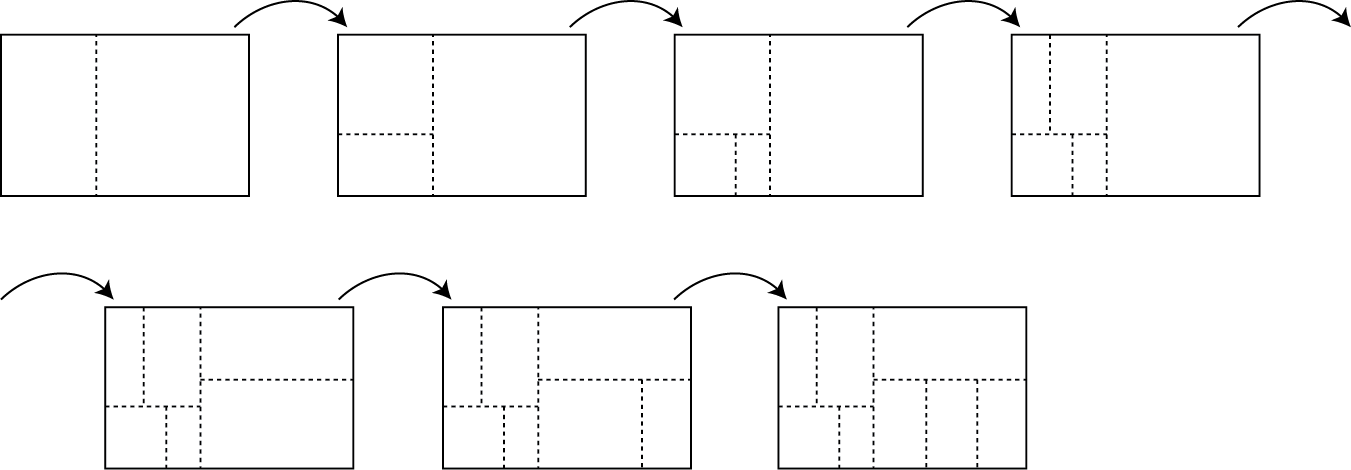
Ko si uspel izrisati gornjo sliko (seveda bo pri tebi drugačna - in to vsakič, ko znova poženeš program), dodaj še fotografije. Te vstaviš v pravokotnike, ki jih ne moreš več rezati. Postavi jih na sredo pravokotnika (predpostavi, da je velikost slike 100x100 točk). Tako kot v prejšnji nalogi uporabi slike iz trenutnega direktorija. Slike morajo biti naključno premešane. Vsaka se sme pojaviti samo enkrat. Če jih zmanjka, pusti preostale pravokotnike prazne. Če je slik preveč, odvečnih slik ne prikaži.
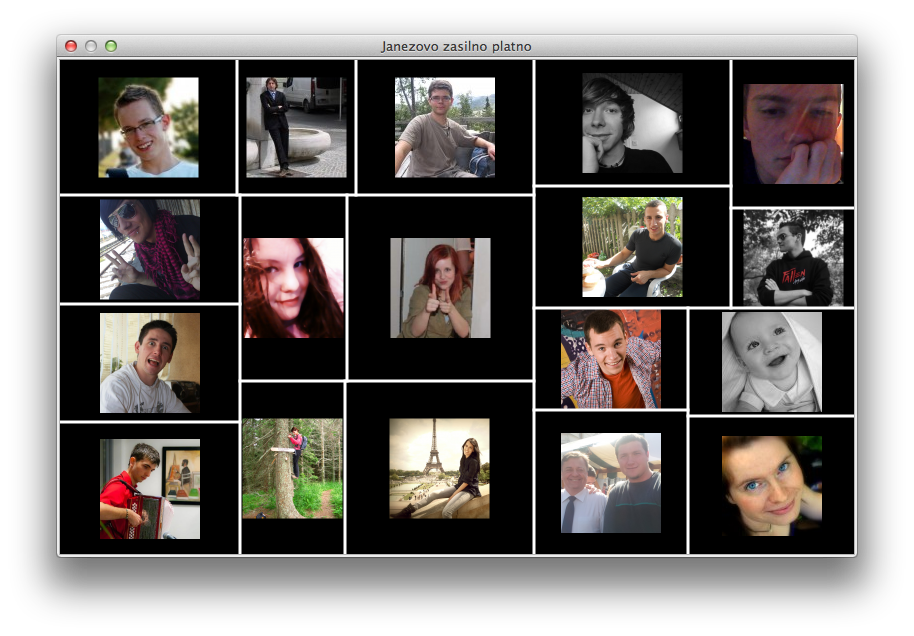
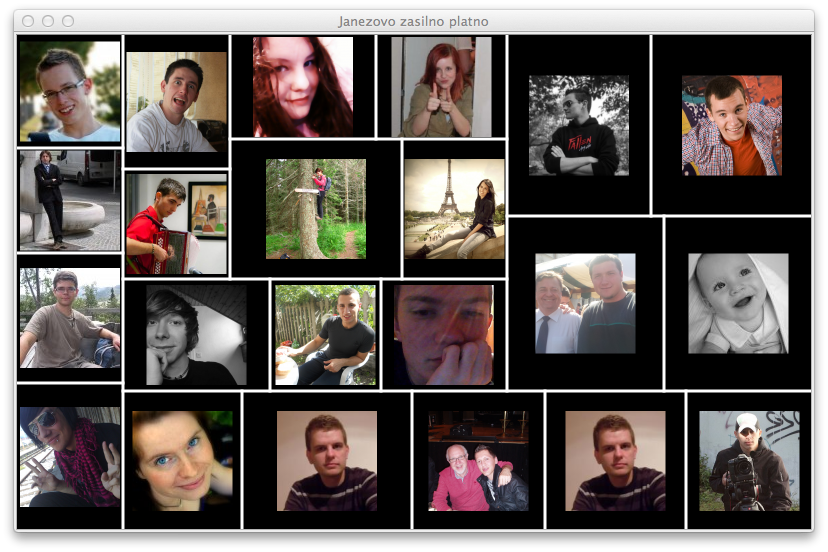
Rešitev
Ogrevalna naloga: izpis številk in koordinat
Ogrevalna naloga navadno predstavlja korak proti rešitvi "prave". Tudi tokrat je bilo sicer tako, vendar bi lahko pravo brez večjih težav rešili tudi brez ogrevalne. Pač pa je bil namen ogrevalne naloge, da vam pomaga, da bi pravo nalogo rešili elegantneje, kot bi jo sicer.
Poskušal sem vam pokazati, da lahko koordinate slike (ki jih morate računati
v pravi nalogi) brez težav izračunate iz zaporedne številke slike. Stolpec je
enak ostanku po deljenju zaporedne številke s 6, številko vrstice pa dobimo s
celoštevilskim deljenjem s 6. Kadar je ostanek po deljenju s 6 enak 5, je
potrebno iti tudi v novo vrsto, sicer pa ne (end="").
Obvezna naloga: Album
Za rešitev sem oglašal, da je dolga (izvzemši importe) samo
štiri vrstice. Je, vendar bi morali programirati malo grše, kot hočemo;
problem je v filtriranju (hočemo samo PNG-je) in urejanju. Bistveno daljša pa
le ni.
Prvi del je nekaj, kar bi moralo biti po nalogi "Direktoriji" trivialno: izberemo vse datoteke s končnico png, jih uredimo in potem vzamemo samo prvih 24.
Drugi del so tiste "štiri vrstice". Spremenljivki i in
fn vsebujeta zaporedno številko in ime datoteke (Guido, hvala
za enumerate!). Iz zaporedne številke izračunamo koordinate
ter postavimo v okno sliko in podnapis.
Dodatna naloga: Kolaž
Ta naloga pa je predvsem vaja iz rekurzije. Malo spominja na trikotnik Sierpinskega. Nekoliko lažja je, ker je lažje preračunavati koordinate, istočasno pa nekoliko težja, ker je potrebno obračati smer. Tole rešitev vsekakor dobro preberite, če se slučajno prikrade kaj podobnega na izpit.
Poglejmo najprej spodnji del: spet zložimo imena vseh datotek s slikami
v seznam, le da ga zdaj naključno premešamo. Nato pokličemo rekurzivno funkcijo
kolaz. Ta bo imela pet argumentov (v prvem koraku lahko zadnjega,
seznam slik, izpustimo). Prvi štirje so koordinate pravokotnika, ki ga je
potrebno razdeliti. Naslednji argument pove, ali ga je potrebno razdeliti z
navpično črto; to je lahko res ali ne (True ali False).
Zadnji je premešani seznam slik.
Funkcija dela takole: najprej preveri, ali je pravokotnik slučajno že
premajhen, da bi ga delili v katerikoli smeri. Če je tako, pogleda, ali imamo
še kakšno sliko (lahko bi jih tudi že zmanjkalo...). Če jo imamo, jo vstavi.
Do slike pride s slike.pop(), ki vrne zadnjo sliko na seznamu in
jo odstrani z njega - natačno tisto, kar potrebujemo.
Če pravokotnik še ni premajhen, preveri, ali ga je potrebno razdeliti v
navpični smeri. Če je tako, preveri, ali ga je sploh še mogoče deliti v
navpični smeri. Če je še dovolj velik, izbere koordinato, kjer bo potegnil
navpično črto; ta mora biti med x0+100 in x1-100,
da bo dovolj daleč od roba. Koordinati y sta seveda takšni, kot smo ju dobili
ob klicu funkcije. Potegne torej črto, potem pa pokliče funkcijo
kolaz (torej samo sebe) dvakrat - enkrat za levi, enkrat za desni
pravokotnik. Pozorno poglejte in razmislite koordinate! Bodite tudi pozorni
na to, kaj storimo z argumentom, ki določa smer: obrnemo ga. Ker vemo, da je
True, bi sicer lahko namesto not navp pisali tudi
False.
Če je pravokotnik premajhen, da bi ga delili z navpično črto, ga bomo z
vodoravno. To naredimo tako da, preprosto, ponovno pokličemo kolaz
z enakimi argumenti, le smer obrnemo.
V drugi polovici funckije naredimo isto še za delitev z vodoravno črto.
Funkcijo bi bilo možno napisati z manj klici kolaz. Vendar bi
bila potem najbrž bolj in ne manj zapletena.