Testi

Testi: testi-podjetne-cebele.py

Naloga

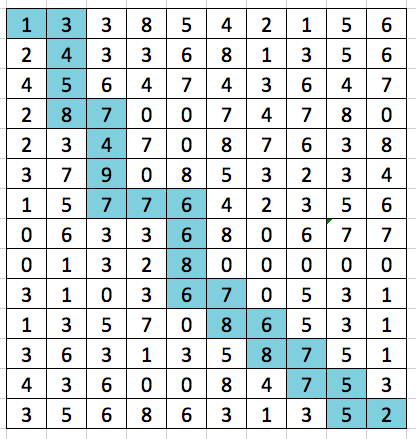
Rože v neki deželi so posajene v pravokotno mrežo. Čebelam je pomembno, koliko nektarja je v posameznem cvetu. Na desni je slika, ki kaže količino nektarja v cvetovih nekega vrta (v miligramih), še desno desno pa seznam seznamov, s kakršnim programiranja vešče čebele shranijo stanje.

Na podoben način shranjujejo stanje vseh drugih vrtov. Vrtovi so lahko različnih velikosti - nekateri imajo tudi le po eno vrsto ali en stolpec rož, pa tudi količina nektarja v rožah je lahko poljubno pozitivno število. Lahko se zgodi celo, da ima vrt en sam cvet.

Koordinatni sistem, ki ga uporabljajo čebele, je takšen, da je točka (0, 0) v zgornjem levem (ne spodnjem levem!) vogalu. Ko gre čebela navzdol, koordinata y narašča: če čebela odleti, recimo, za eno vrstico nižje, se koordinata y poveča za 1.

 
   [[1,3,3,8,5,4,2,1,5,6],
    [2,4,3,3,6,8,1,3,5,6],
    [4,5,6,4,7,4,3,6,4,7],
    [2,8,7,0,0,7,4,7,8,0],
    [2,3,4,7,0,8,7,6,3,8],
    [3,7,9,0,8,5,3,2,3,4],
    [1,5,7,7,6,4,2,3,5,6],
    [0,6,3,3,6,8,0,6,7,7],
    [0,1,3,2,8,0,0,0,0,0],
    [3,1,0,3,6,7,0,5,3,1],
    [1,3,5,7,0,8,6,5,3,1],
    [3,6,3,1,3,5,8,7,5,1],
    [4,3,6,0,0,8,4,7,5,3],
    [3,5,6,8,6,3,1,3,5,2]]

Za ogrevanje

Napišite funkcijo naj_koordinate(vrt), ki vrne koordinato "najbogatejšega" cveta. V gornjem primeru mora funkcija vrniti (2, 5) (kot terko dveh int-ov), saj je tam cvet z 9 mg nektarja. Če sta na vrtu dva cveta z največjo količino nektarja, naj vrne tistega, ki je višje. Če sta dva na isti višini, naj vrne tistega, ki je bolj levo.

Za oceno 6

Čebele opisujejo pot z zaporedjem znakov "L", "R", "U" in "D" (kot left, right, up in down; angleške črke uporabljamo, ker se "desno" in "dol" v slovenščini začneta z isto črko). Pri tem D pomeni, da se koordinata y poveča za 1 (čebela gre eno vrstico nižje).

Obiranje cvetov se vedno začne pri cvetu (0, 0).

Napišite funkcijo pravilna_pot(pot, vrt), ki prejme niz, ki opisuje pot (npr. "RRDDRLL") in vrt. Kot rezultat naj vrne True, če je pot pravilna in False, če ni. Pot ni pravilna, če čebela na njej kdaj zapusti vrt. Primeri nepravilnih poti za gornji vrt so, recimo "DDRRRRRRRRRRRRRRRRRRRRRRR" (čebelo odnese nekam na levo) in "U" (čebelo takoj odpihne navzgor).

Za oceno 7

Napišite funkcijo dobicek_na_poti(pot, vrt), ki pove, koliko nektarja bo čebela nabrala, če leta od cveta do cveta, kot ji veleva pot. Predpostaviti smete, da je pot nikoli ne bo vodila na cvet, ki ga je že obrala. Pot je tudi gotovo pravilna in nikoli ne vodi izven vrta.

Če na gornjem travniku preleti pot "RDDL" bo nabrala 17 mg nektarja (pri izračunu je potrebno upoštevati tako prvi kot zadnji cvet).

Za oceno 8

Napišite funkcijo brez_ponovitve(pot), ki vrne True, če čebela, ki leti po podatni poti, nikoli ne obišče dvakrat (ali večkrat) istega cveta.

Za oceno 9

V tej deželi je pogosto močan veter, zaradi katerega lahko čebele letajo le navzdol in desno. Napišite funkcijo najboljsa_pot(vrt), ki za podani vrt vrne največjo količino nektarja, ki jo je mogoče nabrati na ta način (se pravi s potjo, ki vedno gre le desno in navzdol).

Za gornji primer mora funkcija vrniti 136. Toliko nabere čebela, če gre po poti na spodnji sliki.

Kako se reši to nalogo, bom/sem povedal na predavanjih.

Za oceno 10

Neka čebela se je odločila, da na svoji poti nikoli ne bo šla z nekega cveta na drugi cvet, ki bi imel samo toliko (ali celo manj) nektarja kot trenutni cvet. Z drugimi besedami, količina nektarja, ki ga srečuje na cvetovih na svoji poti mora od cveta do cveta naraščati. Napišite funkcijo naj_narascajoca(vrt), ki kot argument dobi vrt, kot rezultat pa vrne najdaljšo možno pot te čebele v podanem vrtu.

Za gornji vrt lahko funkcija vrne poti "RDDRDL", "DRDRDL" ali "DDRRDL".

Za oceno 11

(Saj ni toliko težja, samo en argument več boste najbrž morali vleči skozi funkcijo.)

Neka malenkost manj požrešna čebela je zadovoljna tudi, če gre s trenutnega cveta na cvet, ki ima "samo" enako količino nektarja. Napišite funkcijo naj_nepadajoca(vrt), ki vrne najdaljšo možno pot te čebele v podanem vrtu.

Za gornji vrt sta enako dobra dva odgovora, namreč "RRDLDRDL" in "RRDRDLDL".

Preproste rešitve

Najbogatejši cvet

Priporočil sem, da za začetek napišete funkcijo, ki vrne indeks največjega elementa. Tipično se imenuje argmax. Če predpostavimo, da so vsi elementi nenegativni, bi lahko bila takšna:

def argmax(s): naj = naj_idx = -1 for i in range(len(s)): if s[i] > naj: naj, naj_idx = s[i], i return naj_idx

Veliko lepše pa je, če se spomnimo funkcije enumerate, s katero bomo hkrati dobili indeks in vrednost:

def argmax(s): naj = naj_idx = -1 for e, i in enumerate(len(s): if e > naj: naj, naj_idx = e, i return naj_idx

Za domačo nalogo je bilo potrebno narediti skoraj isto, le z dvema indeksoma.

def naj_koordinate(vrt): naj_dob = naj_x = naj_y = -1 for y, vrsta in enumerate(vrt): for x, dobicek in enumerate(vrsta): if dobicek > naj_dob: naj_dob, naj_x, naj_y = dobicek, x, y return naj_x, naj_y

Pravilnost poti

Za to nalogo in za prihodnje si bomo pripravili priročen slovar, v katerem bo pisalo, za koliko posamezna črka spremeni koordinati x in y.

premiki = {"D": (0, 1), "U": (0, -1), "L": (-1, 0), "R": (1, 0)}

S tem slovarjem bo čebelji let vedno sprogramiran po tem vzorcu:

x = y = 0 for korak in pot: dx, dy = premiki[korak] x += dx y += dy

Začetni koordinati sta x = y = 0. Za vsak korak na poti (for korak in pot), preberemo spremembo x in y (dx, dy = premiki[korak]) in ustrezno povečamo (ali zmanjšamo, če sta premika negativna) x in y (x += dx; y + = dy).

Naloge za ocene 6, 7 in 8 se razlikujejo le po tem, kaj še počnemo znotraj zanke. Pri pravilna_pot gledamo, ali so koordinate slučajno izven vrta in v tem primeru takoj zatulimo Fouš! Če se vse lepo izteče, vrnemo True.

def pravilna_pot(pot, vrt): visina = len(vrt) sirina = len(vrt[0]) x = y = 0 for korak in pot: dx, dy = premiki[korak] x += dx y += dy if not (0 <= x < sirina and 0 <= y < visina): return False return True

Dobiček

V nalogi za računanje dobička v vsakem koraku prištejemo vrednost v trenutnem cvetu.

def dobicek_na_poti(pot, vrt): dobicek = vrt[0][0] x = y = 0 for korak in pot: dx, dy = premiki[korak] x += dx y += dy dobicek += vrt[y][x] return dobicek

Brez ponovitve

V nalogi, kjer nas zanima, ali smo določen cvet obiskali večkrat, si pripravimo množico, v katero bomo shranjevali koordinate obiskanih cvetov. Znotraj zanke preverimo, ali je ta cvet že v množici in v tem primeru vrnemo False. Če se vse lepo izteče, vrnem True.

def brez_ponovitve(pot): x = y = 0 obiskana = {(x, y)} for korak in pot: dx, dy = premiki[korak] x += dx y += dy if (x, y) in obiskana: return False obiskana.add((x, y)) return True

Najboljša pot

Ta funkcija je nekoliko sitna: veliko prijetneje bi jo bilo sprogramirati z uporabo kake knjižnice za delo z matrikami, kot recimo numpy. A to je iz čisto drugega vica in ne sodi v Programiranje 1 (tistim, ki se dolgočasite, pa definitivno priporočam ogled).

Tule je funkcija, ki dela točno to, kar sem risal na predavanjih. Najprej pripravi eno tabelo ničel, ki je enako velika kot vrt. Potem najprej sešteje prvo vrstico, nato pa gre po vrsticah. V vsaki najprej izračuna vrednost prvega elementa, nato nadaljuje proti desni, tako da pogleda dobiček na levi in zgoraj, vzame večjega od njiju ter prišteje trenutni cvet.

def najboljsa_pot(vrt): visina = len(vrt) sirina = len(vrt[0]) dobicki = [] for y in range(visina): dobicki.append([0] * sirina) dobicki[0][0] = vrt[0][0] for x in range(1, sirina): dobicki[0][x] = dobicki[0][x - 1] + vrt[0][x] for y in range(1, visina): dobicki[y][0] = dobicki[y - 1][0] + vrt[y][0] for x in range(1, sirina): dobicki[y][x] = max(dobicki[y][x - 1], dobicki[y - 1][x]) + vrt[y][x] return dobicki[-1][-1]

Vsaj malo lepše je tole: namesto, da bi pripravili tabelo ničel, skopiramo vrt. Kot so odkrili kolegi, deepcopy ne dela čisto, ker sem pregrdo sestavljal primere. Kopijo lahko sestavimo, recimo, z appendom; šlo bi tudi preprosteje, vendar tega še ne znamo.

def naj_pot(vrt): visina = len(vrt) sirina = len(vrt[0]) dobicki = [] for vrsta in vrt: dobicki.append(list(vrsta)) for x in range(1, sirina): dobicki[0][x] += dobicki[0][x - 1] for y in range(1, visina): dobicki[y][0] += dobicki[y - 1][0] for x in range(1, sirina): dobicki[y][x] += max(dobicki[y][x - 1], dobicki[y - 1][x]) return dobicki[-1][-1]

Tole je pa spodobna rešitev - s trikom. Za dobičke ne naredi tabele ničel, temveč jih sestavlja sproti. Trik je v tem, da jim doda še eno vrstico zgoraj in en stolpec na levi. Vanj napiše same ničle. Zdaj ni več potrebno posebej, obravnavati prve vrstice ali stolpca, temveč preprosto vedno gledamo zgornji in levi cvet, saj bosta vedno obstajala.

Ko sestavljamo novo vrsto dobičkov, jo zapisujemo v vrstico nova. Ta ima prej omenjeni levi stolpec; ko vrstico dodamo na konec tabele z dobički, levi stolpec odstranimo. To nam omogoča, da gremo z zanko for istočasno prek cvetov v tej vrsti vrta in dobičkov iz prejšnje vrstice, for cvet, zgoraj in zip(vrsta, dobicki[-1]). Rezultat je kar elegantna funkcija.

def najboljsa_pot(vrt): dobicki = [[0]*len(vrt[0])] for vrsta in vrt: nova = [0] for cvet, zgoraj in zip(vrsta, dobicki[-1]): nova.append(max(nova[-1], zgoraj) + cvet) dobicki.append(nova[1:]) return dobicki[-1][-1]

Najdaljša naraščajoča pot

Tole je pa čisto lepa rekurzija: za vsako sobo poskusimo premike v vse možne smeri (najdemo jih kar v premiki.items()). Če so legalni (niso izven vrta in je količina nektarja v tamkajšnjem cvetu večja kot v trenutnem), je najdaljša pot, ki jo lahko naredimo v ono smer, enaka koraku v ono smer + najdaljša pot, ki jo lahko naredimo od onega cveta. Če je ta pot daljša od najdaljše doslej najdene, si jo zapomnimo. Na koncu vrnemo najdaljšo pot, seve.

def naj_narascajoca(vrt, x=0, y=0): visina = len(vrt) sirina = len(vrt[0]) trenutni = vrt[y][x] naj_naprej = "" for korak, (dx, dy) in premiki.items(): nx, ny = x + dx, y + dy if 0 <= nx < sirina and 0 <= ny < visina and vrt[ny][nx] > trenutni: naprej = korak + naj_narascajoca(vrt, nx, ny) if len(naprej) > len(naj_naprej): naj_naprej = naprej return naj_naprej

Uporabili smo še en trik: ob rekurzivnem klicu moramo povedati tudi, v kateri sobi začnemo. Zato potrebujemo argumenta x in y. Damo pa jima privzeto vrednost 0, saj naj bi funkcija po definiciji vedno začenjala iz (0, 0).

Najdaljša nepadajoča pot

Tole je podobno kot prej, paziti moramo smo, da ne bi slučajno prišli v sobo, v kateri smo že bili (in se zaciklali). Zato dodamo še en argument, množico že obiskanih cvetov. Ko preverjamo premike, po novem preverimo tudi, ali je cvet, na katerega se podajamo, še neobiskan. Ob rekurzivnem klicu funkcije podamo množico, ki poleg obstoječih elementov vsebuje še sobo, v katero gremo. (Tu se splača spomniti, kako se imenuje operator, ki računa unijo: |.)

def naj_nepadajoca(vrt, x=0, y=0, obiskane=frozenset({(0, 0)})): visina = len(vrt) sirina = len(vrt[0]) trenutni = vrt[y][x] naj_naprej = "" for korak, (dx, dy) in premiki.items(): nx, ny = x + dx, y + dy if 0 <= nx < sirina and 0 <= ny < visina and (nx, ny) not in obiskane and vrt[ny][nx] >= trenutni: naprej = korak + naj_nepadajoca(vrt, nx, ny, obiskane | {(nx, ny)}) if len(naprej) > len(naj_naprej): naj_naprej = naprej return naj_naprej

Zakaj smo kot privzeto vrednost navedli zamrznjeno množico, frozenset({0, 0}), in ne kar običajne množice, {(0, 0)}. Funkcija lahko spremeni lastne privzete vrednosti. To se šteje za grdo in nevarno. Zato je zelo priporočljivo, da so privzete vrednosti konstantne. Okolja, ki preverjajo pravilnost programov, kot recimo PyCharm, bi postala živčna, čim bi videla, da kot privzeto vrednost uporabljamo navadno množico - čeprav to sicer smemo storiti in tudi deluje.

Generatorji poenostavijo rešitve nalog 6 - 8

Na predavanjih, ki so sledila tistim, na katerih ste dobili to domačo nalogo, smo se učili o generatorjih. Z njimi si lepo poenostavimo rešitve nalog od 6 do 8.

Najprej napišemo generator, ki kot argument dobi pot in vrača koordinate na tej poti. Generator ne potrebuje vrta.

premiki = {"D": (0, 1), "U": (0, -1), "L": (-1, 0), "R": (1, 0)} def prehodi(pot): x = y = 0 yield x, y for korak in pot: dx, dy = premiki[korak] x += dx y += dy yield x, y

Funkcije za oceno 6 - 8 gredo prek koordinat, ki jih generira gornji generator in z njimi počne, kar je treba - prva preverja pravilnost, druga sešteva dobiček, tretja preverja, ali smo določeno polje že videli.

def pravilna_pot(pot, vrt): visina = len(vrt) sirina = len(vrt[0]) for x, y in prehodi(pot): if not (0 <= x < sirina and 0 <= y < visina): return False return True def dobicek_na_poti(pot, vrt): dobicek = 0 for x, y in prehodi(pot): dobicek += vrt[y][x] return dobicek def brez_ponovitve(pot): obiskana = set() for x, y in prehodi(pot): if (x, y) in obiskana: return False obiskana.add((x, y)) return True

Lepota teh funkcij je v tem, da vsaka res dela samo tisto, kar je zanjo specifično, zato so preglednejše. Vsa skupna koda, ki se ukvarja samo s spreminjanjem koordinat, je umaknjena v generator.

Rešitve v eni vrstici

Letos jih malo zanemarjam. Pa si dajmo malo duška.

Recimo, da imamo tole pripravljeno (če ne bi imeli, se da vtlačiti v eno vrstico, vendar ... nima smisla težiti s tem.

from functools import reduce premiki = {"D": (0, 1), "U": (0, -1), "L": (-1, 0), "R": (1, 0)}

Poleg tega predpostavimo, da imamo generator prehodi, kot smo ga definirali zgoraj. Pravzaprav ne, to bi bila goljufija. Imejmo funkcijo prehodi, ki je takšna

def prehodi(pot): return reduce(lambda s, m: s + [(s[-1][0] + premiki[m][0], s[-1][1] + premiki[m][1])], pot, [(0, 0)])

Funkcija vrne seznam koordinat, prek katerih nas vodi pot.

V spodnjih funkcijah bomo klicali gornjo funkcijo, da bodo vrstice nekoliko krajše. Če bi hoteli programe zares napisati v eni vrstici, bi pač namesto klica gornje funkcije preprosto prekopirali njeno kodo.

Zdaj pa gremo:

# 5 def naj_koordinate(vrt): return tuple(-i for i in max((dobicek, -y, -x) for y, vrsta in enumerate(vrt) for x, dobicek in enumerate(vrsta))[2:0:-1]) # 6 def pravilna_pot(pot, vrt): return all(0 <= x < len(vrt[0]) and 0 <= y < len(vrt) for x, y in prehodi(pot)) # 7 def dobicek_na_poti(pot, vrt): return sum(vrt[y][x] for x, y in prehodi(pot)) # 8 def brez_ponovitve(pot): return len(set(prehodi(pot))) == len(pot) + 1 # 9 def najboljsa_pot(vrt): return reduce(lambda d, v: d + [reduce(lambda s, x: s+[max(s[-1], x[1]) + x[0]], zip(v, d[-1]), [0])[1:]], vrt, [[0]*len(vrt[0])])[-1][-1] # 10 in 11 # Ne da se mi, najbrž je itak pregrdo, da bi bilo vredno. ;)

Funkcije so pravzaprav čisto berljive. Ona za oceno 5 sestavi terke (dobiček, -y, -x), jih uredi od največje proti najmanjši ter vrne koordinate iz prve. Kompliciranje z minusi in obračanjem je potrebno, ker v primeru enako bogatih cvetov vračamo tistega z najmanjšo koordinato, ne največjo.

Funkcija za oceno 6 pravi, da morajo biti vse (all) koordinate znotraj meja. Funkcija za oceno 7 sešteje (sum) donose cvetov. Funkcija za oceno 8 preveri, ali je množica obiskanih cvetov enaka dolžini poti + 1. Če ni, smo enega od cvetov obiskali večkrat.

Funkcijo za izračun najboljše poti dobimo tako, da stisnemo elegantnejšo različico funkcije, ki smo jo napisali zgoraj. Metoda, kako se to stisne, je čisto preprosta, samo dva klasična trika uporabiš. Rezultat pa je žal popolnoma nepregleden, tako da ga ni vredno komentirati.

Kot rečeno, bi lahko funkcije 6 - 8, ki uporabljajo funkcijo prehodi, napisali tudi brez nje. Le malo manj pregledno bi bilo:

def pravilna_pot(pot, vrt): return all(0 <= x < len(vrt[0]) and 0 <= y < len(vrt) for x, y in reduce(lambda s, m: s + [(s[-1][0] + premiki[m][0], s[-1][1] + premiki[m][1])], pot, [(0, 0)])) def dobicek_na_poti(pot, vrt): return sum(vrt[y][x] for x, y in reduce(lambda s, m: s + [(s[-1][0] + premiki[m][0], s[-1][1] + premiki[m][1])], pot, [(0, 0)])) def brez_ponovitve(pot): return len(set(reduce(lambda s, m: s + [(s[-1][0] + premiki[m][0], s[-1][1] + premiki[m][1])], pot, [(0, 0)]))) == len(pot) + 1
Последна промена: среда, 24 март 2021, 23:05