Naloge
Družinsko drevo
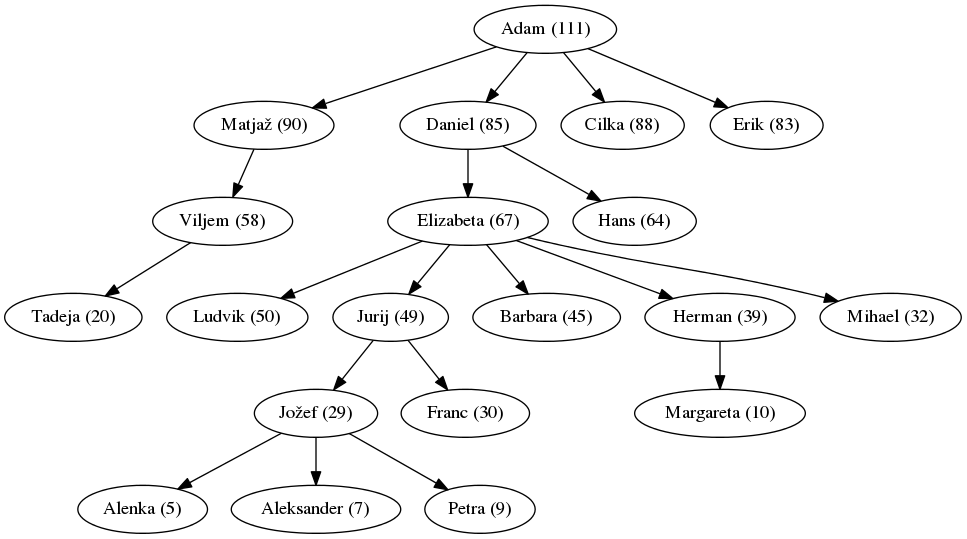
Izpis rodbine
Napišite funkcijo izpis_imen_v_rodbini(ime), ki izpiše vsa imena v določeni rodbini.
>>> izpis_imen_v_rodbini('Hans')
Hans
>>> izpis_imen_v_rodbini('Daniel')
Daniel
Elizabeta
Ludvik
Jurij
Franc
Jožef
Alenka
Aleksander
Petra
Barbara
Herman
Margareta
Mihael
Hans
Rešitev
def izpis_imen_v_rodbini(ime):
print(ime)
for otrok in otroci[ime]:
izpis_imen_v_rodbini(otrok)
Seznam rodbine
Podobno kot prejšnja naloga, le da naj tokrat funkcija imena_v_rodbini(ime) vrne seznam imen v rodbini.
>>> imena_v_rodbini('Hans')
['Hans']
>>> imena_v_rodbini('Daniel')
['Daniel', 'Elizabeta', 'Ludvik', 'Jurij', 'Franc', 'Jožef', 'Alenka', 'Aleksander', 'Petra', 'Barbara', 'Herman', 'Margareta', 'Mihael', 'Hans']
Rešitev
def imena_v_rodbini(ime):
xs = [ime]
for otrok in otroci[ime]:
xs.extend(imena_v_rodbini(otrok))
return xs
Najmlajši
Funkcija najmlajsi_v_rodbini(ime) naj vrne starost in ime najmlajšega člana določene rodbine.
>>> najmlajsi_v_rodbini('Hans')
(64, 'Hans')
>>> najmlajsi_v_rodbini('Daniel')
(5, 'Alenka')
Rešitev
def najmlajsi_v_rodbini(ime):
xs = [(starost[ime], ime)]
for otrok in otroci[ime]:
xs.append(najmlajsi_v_rodbini(otrok))
return min(xs)
Globina
Napišite funkcijo globina_do(od_ime, do_ime), ki pove kako globoko v rodbini osebe od_ime je oseba z imenom do_ime.
>>> globina_do('Daniel', 'Hans')
1
>>> globina_do('Adam', 'Hans')
2
>>> globina_do('Adam', 'Franc')
4
Rešitev
def globina_do(od_ime, do_ime):
if od_ime == do_ime:
return 0
for otrok in otroci[od_ime]:
d = globina_do(otrok, do_ime)
if d is not None:
return d + 1
Pot
Reši podobno nalogo kot je prejšnja, le da naj funkcija pot_do(od_ime, do_ime) ne vrne razdalje do določene osebe, temveč pot do nje.
>>> pot_do('Daniel', 'Hans')
['Daniel', 'Hans']
>>> pot_do('Adam', 'Hans')
['Adam', 'Daniel', 'Hans']
>>> pot_do('Adam', 'Franc')
['Adam', 'Daniel', 'Elizabeta', 'Jurij', 'Franc']
Rešitev
def pot_do(od_ime, do_ime):
if od_ime == do_ime:
return [od_ime]
for otrok in otroci[od_ime]:
d = pot_do(otrok, do_ime)
if d is not None:
return [od_ime] + d
Seznami
Včasih so programerji sestavljali sezname z gnezdenjem terk. Ubogi reveži, druge izbire niso imeli.
Convert
Napiši funkcijo convert(xs), ki seznam xs pretvori v ta arhaični zapis.
>>> convert([])
()
>>> convert([1])
(1, ())
>>> convert([1, 2])
(1, (2, ()))
>>> convert([5, 4, 6, 7, 1])
(5, (4, (6, (7, (1, ())))))
Rešitev
def convert(xs):
if not xs:
return ()
return xs[0], convert(xs[1:])
Dolžina
Napiši funkcijo length(s), ki izračuna dolžino seznama gnezdenih terk.
>>> length(())
0
>>> length((1, ()))
1
>>> length((5, (4, (6, (7, (1, ()))))))
5
Rešitev
def length(xs):
if not xs:
return 0
return 1 + length(xs[1])
Duplikati
Napiši funkcijo dup(s), ki vrne seznam, kjer je vsak element seznama ponovljen dvakrat.
>>> dup((1, (2, ())))
(1, (1, (2, (2, ()))))
>>> dup((5, (4, (6, (7, (1, ()))))))
(5, (5, (4, (4, (6, (6, (7, (7, (1, (1, ()))))))))))
Rešitev
def dup(xs):
if not xs:
return ()
return xs[0], (xs[0], dup(xs[1]))
Reverse
Napiši funkcijo reverse(s), ki vrne obrnjen seznam.
>>> reverse((5, (4, (6, (7, (1, ()))))))
(1, (7, (6, (4, (5, ())))))
Rešitev
def reverse(xs, ys=()):
if xs == ():
return ys
return reverse(xs[1], (xs[0], ys))
Vsota
Napiši funkcijo sum(s), ki sešteje elemente vgnezdenega seznama s.
Pomagajte si s funkcijo isinstance.
>>> isinstance([1, 2, 3], list)
True
>>> isinstance(1, list)
False
>>> sum([])
0
>>> sum([1, 2, 3, 4, 5])
15
>>> sum([1, [], [2, 3, [4]], 5])
15
Rešitev
def sum(xs):
if not xs:
return 0
if isinstance(xs[0], list):
return sum(xs[0]) + sum(xs[1:])
return xs[0] + sum(xs[1:])