Današnja tema je objektno orientirano programiranje (ali, po slovensko, a redkeje uporabljeno, predmetno usmerjeno programiranje). Nekaj terena smo pripravili prejšnjič, v resnici pa med objekti živimo že dolgo, le vedeli nismo zanje, čeprav smo samo besedo "objekt" sem ter tja sramežljivo izrekli. No, v pogostejšo rabo je prišla, ko smo tačeli govoriti o objektih in imenih, a šele danes bo dobila svoj pravi, dokončni pomen.

Na zadnjem predavanju smo risali, a omenili, da v resnici ne rišemo, temveč postavljamo objekte na sliko. Za risanje poskrbi Qt. Vsak objekt na sliki je določene vrste in ima določene lastnosti. Nekatere lastnosti so skupne več vrstam objektov, spet druge so smiselne le za določeno vrsto, zato jo poznajo le ti.

Vrste objektov, s katerimi smo se igrali, so bile črte, točke, krogi in slike. Vsi so imeli koordinate: izvedeli smo jih z metodama x() in y() ter spreminjali z metodo setPos(x, y). Barvo in debelino pa so imele samo črte in krogi, slike pa ne (le metod za nastavljanje barv in debelin vam nisem pokazal, saj stvar ne gre čisto naravnost, s kakimi setColor in setWidth).

Z metodami smo se pravzaprav prvič srečali že davno, ob seznamih. "Lastnost" seznama so pač elementi, ki jih vsebuje, metode, ki jih premore, pa so, recimo, append, count in index. Lastnost niza je prav tako kar njegova vsebina, metode, ki jih ima, pa so, recimo, split, replace in startswith. Kaj so lastnosti datoteke, točneje, spremenljivke tipa file nam je težje uganiti (slutimo pač že: spremenljivka vrste file je nekako vezana na neko datoteko na disku, torej je lastnost ta "povezava", poleg tega pa si mora zapomniti vsaj še, do kje je datoteka že prebrana).

Danes bomo prvič sestavili nov podatkovni tip, novo vrsto spremenljivke. "Tipom" - kot so na primer int, float, list, file in QGraphicsItemLine - pravimo razredi in vrednostim - posamezni številki, seznamu, datoteki, črti - pravimo objekti. Naš današnji podatkovni tip bo Turtle.

Nekaj o jeziku programov: doslej smo programirali tako, da smo imena spremenljivk in funkcij pisali v slovenščini. Dasiravno je to, kljub svojih arhaizmom in celo prav zavoljo njih, moj najljubši jezik, vam priporočam: programirajte v angleščini. Še vedno, kadar sem se lotil pisati slovenske spremenljivke, se je končalo s čubodro, že zato, ker ob svoji kodi vedno uporabljamo tudi tujo in še svoje stare knjižnice, ki smo jih iz takšnih in drugačnih razlogov morali pisati v angleščini. Tudi pri tem predmetu bomo poslej vedno pogosteje posegli po angleških imenih.

Želva

Objekt vrste Turtle naredimo tako, da rečemo, recimo

t = Turtle() S t = Turtle() smo skonstruirali novo želvo in jo priredili spremenljivki t.

Želva lahko naredi podano število korakov naprej ali nazaj, tako da pokličemo njeni metodi forward(s) (v našem primeru, ko imamo želvo t, bomo rekli, recimo, t.forward(10) in backward(s); x je število korakov v točkah (pikslih). Zna se tudi obračati; pokličemo lahko turn(phi), kjer je phi kot v stopinjah, pri čemer so pozitivni koti v smeri urinega kazalca (da ne bo preveč preprosto!). Poleg ima tudi metodi left() in right(), ki obrneta želvo za 90 stopinj v levo in desno. V začetku je želva na sredi okna in gleda navzgor. Če jo želimo premakniti in preobrniti, pokličemo fly(x, y, phi); ta želvo odnese na postavljene koordinate in jo obrne v želeno smer. Kot 0 stopinj kaže navzgor.

Želva ima tudi pero, ki je lahko spuščeno ali dvignjeno, tako da želva vleče (ali pa ne) za seboj črto. V začetku je spuščeno; dvignemo ga s pen_up() in spustimo s pen_down()

Pa še par nerisarskih zadev. Želvi lahko rečemo, naj malo počaka, tako da pokličemo metodo wait(t). Kot argument povemo čas čakanja v sekundah. Lahko pa ji naročimo, naj počaka po vsakem risarskem ukazu, tako da pokličemo metodo setPause(t). Pri tem t spet pove čas v sekundah. Če se čakanja naveličamo, pokličemo noPause().

Želva je na sliki vidna. Če jo želimo skriti, pokličemo hide(), s show() pa jo spet prikličemo.

Tule je še enkrat ves seznam:

  • forward(s), backward(s) pojdi s točk naprej oz. nazaj
  • turn(phi) obrni se za phi stopinj v smeri urinega kazalca
  • left(), right() obrni se za 90 stopinj levo oz. desno
  • fly(x, y, phi) poleti na koordinati x, y in se obrni v smer phi
  • pen_up(), pen_down() dvigni oz. spusti pero
  • wait(t) počakaj t sekund
  • set_pause(t), no_pause() nastavi oz. prekliči čakanje po vsakem ukazu
  • hide(), show() pokaži oz. skrij želvo

V vsej svoj prizemeljski preprostosti je želva imenitna žival. Narisati zna, recimo, kvadrat, recimo s stranico 100, tako da gre štirikrat naprej za 100 točk in se nato obrne levo:

for i in range(4): t.forward(100) t.left() Veste, kaj? Tole spravimo kar v funkcijo. def square(turtle, a): for i in range(4): turtle.forward(a) turtle.left() Funkcija pričakuje dva argumenta, želvo, s katero naj riše, in dolžino stranice.

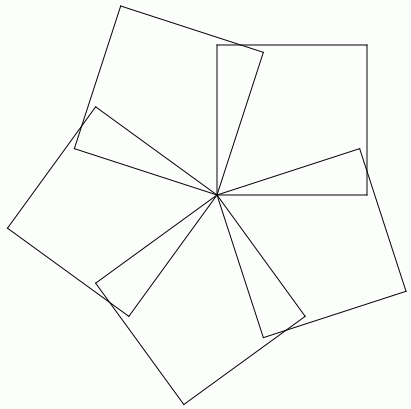
Pri funkciji square je posebej zanimivo in dobrodošlo, da je želva po risanju kvadrata obrnjena natanko tako, kot je bila pred njim. To nam omogoča takšnole igro: narišemo kvadrat, nato nekoliko zasukamo želvo, narišemo nov kvadrat, spet zasukamo in to ponavljamo toliko časa, dokler ne pridemo naokrog. Na spodnjih slikah je 5 kvadratov, zasukanih za 72 stopinj in 90 kvadratov zasukanih za 4 stopinje.

for i in range(5): square(turtle, 150) turtle.turn(72)
for i in range(90): square(t, 150) t.turn(4)

Ob funkciji za kvadrat se hitro domislimo, kako risati mnogokotnike. Namesto štirih bomo naredili k korakov, v vsakem koraku bomo nagnali želvo za določeno razdaljo naprej in jo obrnili za ... koliko? Za koliko stopinj se moramo obrniti, da narišemo šestkotnik? Nobene posebne geometrije ne potrebujemo, če se spomnimo, da moramo biti na koncu obrnjeni tja, kot smo bili v začetku. Poln kot ima 360 stopinj, za šestkotnik se bomo v vsakem od šestih korakov obrnili za 60 stopinj. Za k-kotnik pa za 360/k.

def polygon(turtle, a, k): for i in range(k): turtle.forward(a) turtle.turn(360. / k)

S funkcijo brez znoja narišemo sedemkotnik, le polygon(t, 50, 7) pokličemo. Tudi risanje snežink je z želvo trivialno: poženemo jo za določeno razdaljo naprej, ji rečemo, naj pride nazaj; to ponovimo k-krat, vmes pa jo obračamo za kot 360/k.

def flake(turtle, a, k): for i in range(k): turtle.forward(a) turtle.backward(a) turtle.turn(360. / k) Funkciji za risanje mnogokotnika in snežinke sta si simpatično podobni. Razlika je le v tem, da enkrat začnemo v vogalu mnogokotnika, drugič v središču snežinke. Polmer snežinke je enak podani dolžini l, pri mnogokotniku pa je l dolžina stranice.

Ob snežinki navrzimo, brez posebne razlage, še funkcijo, ki izriše lepšo snežinko, tako ki je definirana tako, da iz vsakega kraka gledata še po dva kraka, pod kotoma 30 stopinje levo in desno ter z dolžino f-krat (npr. 2-krat ali 1.4-krat krajšo) od kraka, iz katerega izvirata. Podkraka pa imata svoja podpodkraka, ti imajo podpodpodkrake in tako naprej, dokler njihove dolžine niso krajše od 5 točk.

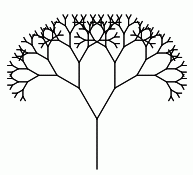def krak(turtle, a, f=2.): turtle.forward(a) if a > 5: turtle.turn(30) krak(turtle, a / f, f) turtle.turn(-60) krak(turtle, a / f, f) turtle.turn(30) turtle.backward(a)
En krak, f = 1.4

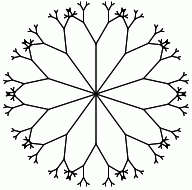f = 2

f = 1.4

Najlepše snežinke pa nam z želvo skuha Koch.

def broken_line(turtle, length): if length < 5: turtle.forward(length) else: broken_line(turtle, length / 3.) turtle.turn(-60) broken_line(turtle, length / 3.) turtle.turn(120) broken_line(turtle, length / 3.) turtle.turn(-60) broken_line(turtle, length / 3.) t = Turtle() t.fly(100, 120, 90) broken_line(t, 400) t.turn(120) broken_line(t, 400) t.turn(120) broken_line(t, 400)

Dovolj igranja. Da je želva koristna žival, sem vas menda prepričal. Zdaj pa jo sprogramirajmo.

Trop želv

Še prej pa naredimo le še eno nepomembno vajo, ki nam bo pomagala razmišljati. Sestavimo ne eno, temveč pet želv in jih v začetku obrnimo v naključne smeri. Nato stokrat naključno izberimo eno od želv, jo obrnimo za naključen kot med -30 in +30 stopinj ter pošljimo deset točk naprej.

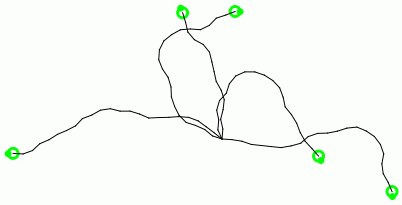
import random turtles = [] for i in range(5): t = Turtle() t.turn(360 * random.random()) turtles.append(t) for i in range(100): t = random.choice(turtles) t.turn(-30 + 60 * random.random()) t.forward(10) t.wait(0.5) t.wait()

Nič takega, nič posebno lepega nismo narisali. Namen vaje je le, da si pravilno predstavljate, da je želv lahko tudi več.

Razred Turtle

Začnimo takole: katere podatke mora shranjevati (vsaka) želva, da lahko deluje? Vedeti mora

  • kje je; to bomo shranili v x in y
  • kam je obrnjena: to bomo shranili v angle
  • ali je pero spuščeno ali dvignjeno; to bomo shranili v pen_active, ki bo imel vrednost True ali False
Na izrisovanje želv in čakanje po vsakem koraku za zdaj še pozabimo.

Najprej sprejmimo tale dogovor: spremenljivki, ki je vsebovala želvo, smo doslej rekli t, kadar je šlo za argument funkcije, pa smo jo imenovali turtle. Poslej ji bomo iz razlogov, ki bodo kmalu jasni, namesto t ali turtle rekli self. Želva, self, bo torej vsebovala svoje koordinate, kot in stanje peresa. Vse to bo shranjeno v self.x, self.y, self.angle in self.pen_active; tem rečem bomo rekli atributi razreda Turtle. Atribut so nekateri želeli sloveniti v lastnost, pa se ni prijelo. V nekaterih programskih jezikih se skoraj isti stvari reče polje ali, po angleško field.

Kako bi bila videti funkcija, ki nastavi pravilne začetne vrednosti vseh teh atributov? Imenujmo jo - spet iz razlogov, ki bodo jasni čez nekaj vrstic - __init__. Takšna je.

def __init__(self): self.x, self.y = risar.maxX / 2, risar.maxY / 2 self.angle = 0 self.pen_active = True Nič posebnega ne počne. Kot argument dobi želvo self in ji postavi self.x in self.y na sredo, obrne jo navzgor (self.angle = 0) in spusti pero.

Opogumljeni s preprostostjo te naloge napišimo še funkcijo forward. Ta bo prejela dva argumenta, želvo (self) in razdaljo, ki naj jo želva prehodi (s).


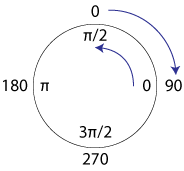
Matematika nam naredi več dela kot programiranje. Najprej moramo spremeniti self.angle v kot, s kakršnim dela računalnik. Glede tega, namreč kota, si smemo čestitati: z njim je narobe natanko vse, kar more biti narobe; je v napačnih enotah (stopinje namesto radianov), 0 kaže v napačno smer (gor namesto desno) in teče v napačno smer (povečuje se v smeri urinega kazalca namesto obratno). Pretvarjanje iz stopinj v radiane prepustimo funkciji radians, naši stari znanki iz "topologije". Da uredimo težavo z ničlo in orientacijo, pa ga odštejmo od 90; 90 poskrbi za začetno smer, minus pa obrne urin kazalec.

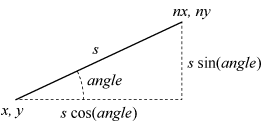
Nato v nx in ny izračunamo, kam je potrebno prestaviti želvo. V smeri x se premaknemo za s * cos(angle) v y za s * sin(angle). Upoštevati moramo še, da računalnikove koordinate tečejo v napačno smer: če želimo gor, moramo odštevati, ne prištevati.

Ko je matematika za nami, je vse preprosto: če je pero spuščeno, narišemo črto, v vsakem primeru, ne glede na pero, pa prestavimo želvo v nove koordinate.

def forward(self, s): angle = radians(90 - self.angle) nx, ny = self.x + s * cos(angle), self.y - s * sin(angle) if self.pen_active: risar.crta(self.x, self.y, nx, ny) self.x, self.y = nx, ny

Napišimo še eno funkcijo: obračanje želve. Ta je trivialna in nevredna komentarja.

def turn(self, angle): self.angle += angle

Skoraj smo že tam, le še zadnji problem rešimo: rekli smo, da bomo napisali razred Turtle in to, kar smo napisali zdaj, ne bodo funkcije kar tako, temveč metode tega razreda. Ne želimo jih klicati z, recimo forward(t, 20), temveč s t.forward(20). Tole pa se naredi takole: zložimo jih v razred.

import risar from math import pi, sin, cos, radians class Turtle: def __init__(self): self.x, self.y = risar.maxX / 2, risar.maxY / 2 self.angle = 0 self.pen_active = True def forward(self, s): angle = radians(90 - self.angle) nx, ny = self.x + s * cos(angle), self.y - s * sin(angle) if self.pen_active: risar.crta(self.x, self.y, nx, ny) self.x, self.y = nx, ny def turn(self, angle): self.angle += angle

S class Turtle: smo napovedali, da sledi definicija razreda. Dvopičju sledi, kot običajno, zamik. Vse, kar je zamaknjeno, so metode razreda. Bi lahko bilo preprosteje?

Zdaj povejmo, kakor smo obljubili, še čemu ravno imeni self in __init__. Prvo pravzaprav ni potrebno. Pisati bi smeli tudi

def turn(zelva, angle): zelva.angle += angle par vrstic višje pa, prav tako brez zadržkov def __init__(ta): ta.x, ta.y = risar.maxX / 2, risar.maxY / 2 ta.angle = 0 ta.pen_active = True Vendar konvencija pravi, da kot ime, ki ga metode uporabljajo za objekt, vedno uporabljamo ime self. (V nekaterih jezikih obstaja this, ki se od Pythonovega self razlikuje po dveh značilnostih: prva je, da nam ga navadno ni potrebno omenjati, druga pa, da mu je vedno ime this. V Pythonu ga moramo omeniti med argumenti, ime pa je načelno poljubno.)

Z __init__ pa je drugače. Ko bomo naredili nov objekt, recimo tako, da bomo poklicali t = Turtle(), bo Python preveril, ali ima razred Turtle metodo z imenom __init__ in jo poklical. Tu glede izbire imena torej nimamo svobode. Metodi __init__ pravimo konstruktor.

Napisani razred že ima vse metode, ki jih potrebuje, z njim lahko z malo iznajdljivosti že rišemo. Kvadrat, recimo, bomo naredili z

t = Turtle() for i in range(4): t.forward(100) t.turn(90) Tako kot prej, torej, le left in right še nimamo, pa se zato znajdemo s turn.

Mimogrede opazimo nekaj zanimivega: funkcija forward je definirana tako, da prejme dva argumenta, self in s. Ob klicu smo podali le drugega, razdaljo, 100. Prvi argument, self se doda avtomatsko - self bo enak objektu, katerega metodo kličemo, v tem primeru t.

Sprogramirajmo backward. Tu nas popade lenoba. Za 42 korakov nazaj gremo lahko preprosto tako, da gremo za -42 korakov naprej, ne? Metoda backward naj torej pokliče kar forward.

def backward(self, s): self.forward(-s) Tule bi morda kdo pričakoval nekaj krajšega: def backward(self, s): forward(-s) Ne v Pythonu. Če hočemo poklicati metodo forward, moramo povedati tudi objekt, čigar forward kličemo. Torej self. forward ni funkcija kar tako. (Nekatere bo to motilo, tudi mene je v začetku, saj sem pred Pythonom znal C++, ki uporablja "krajšo" varianto klicanja metod. Zdaj pa me pravzaprav moti način, v katerem je to narejeno v C++. V Pythonu je iz načina klicanja očitno, da je forward metoda. V C++ pa ni na prvi pogled očitno, ali je forward metoda razreda ali pa morda neka funkcija; da to razčistimo, moramo pogledati v definicijo razreda. Podobno je s self.x, namesto katerega bi v nekaterih jezikih pisali kar x. V Pythonu je očitno, da ne govorimo o nekem x-u kar tako, temveč o atributu, polju objekta.)

Podobno kot backward uženimo še left in right, ki bosta prepustila delo metodi turn. Motivacija je na prvi pogled manjša, saj bi lahko napisali preprosto

def left(self): self.angle -= 90

A ne bomo. Metoda turn, bo kmalu poskrbela še za kaj drugega (konkretno, risanje želve), torej naj za to poskrbi tudi pri obračanju na levo in desno. Naredili bomo torej tako:

def left(self): self.turn(-90) def right(self): self.turn(90)

Le še nekaj drobnarij nam je ostalo: dviganje in spuščanje peresa, letenje in čakanje.

def pen_up(self): self.pen_active = False def pen_down(self): self.pen_active = True def fly(self, x, y, angle): self.x, self.y = x, y self.angle = angle def wait(self): risar.cakaj(s)

Popolna želva

V razred dodajmo še izris želve in čakanje: poučno bo.

Najprej izris. Želvo predstavimo z dvema krogoma, eden ima polmer 10, drugi, ki predstavlja glavo, pa 4. Kroga - kot grafična objekta, takšna, s kakršnimi smo se igrali prejšnjič - bomo shranili v self.body in self.head. Najprej napišimo metodo, ki ju - ob predpostavki, da že obstajata - postavi na ustrezna položaja.

def update(self): angle = radians(90 - self.angle) self.body.setPos(self.x, self.y) self.head.setPos(self.x + 5 * cos(angle), self.y - 5 * sin(angle))

Kot preračunamo tako, kot smo se (nam)učili pri metodi forward. Središče velikega kroga mora biti v self.x in self.y. Manjši krog, glavo, zamaknemo za pet točk v smeri angle. Njegovo središče bo torej v self.x+5*cos(angle), self.y-5*sin(angle), po enaki formuli, kot bi jo uporabili za premik (forward) za pet točk.

Da bo to v resnici delovalo, moramo kroga sestaviti. To seveda storimo ob inicializaciji, v funkciji __init__, ki ji za to dodamo

self.body = risar.krog(0, 0, 5, risar.zelena, 3) self.head = risar.krog(0, 0, 2, risar.zelena, 3) self.update()

Kroga smo postavili kar v (0, 0), potem pa takoj poklicali metodo update(), ki ju prestavi, kamor sodita.

Smo že skoraj na cilju: kroga obstajata in imamo tudi funkcijo, ki ju postavi na pravo mesto. Preostane nam le še, da funkcijo pokličemo vsakič, ko želva spremeni svoje koordinate ali smer. Srečo imamo: ker smo lepo programirali, moramo poklicati je dovolj, da pokličemo update na treh mestih, namreč na koncu metod forward, turn in fly. V metodi backward nam je ni potrebno, saj ta le pokliče forward, v left in right pa tudi ne, saj pokličeta turn.

Za skrivanje in prikazovanje poskrbimo z metodama hide in show, ki ju imajo risarjevi objekti (ali, da si ne lastim zaslug, ki jih nimam, PyQtjevi objekti, ki se skrivajo za risarjem).

def show(self): self.body.show() self.head.show() def hide(self): self.body.hide() self.head.hide()

Ko pokličemo self.body.hide(), veliki krog še vedno obstaja, še vedno se premika naokrog ... le izriše se ne. S self.body.show() pa ga spet pokažemo.

Zdaj pa še čakanje. Koliko sekund naj želva počaka po vsakem koraku, naj pove atribut self.pause. Če ima vrednost 0, ne čakamo; če manjšo od 0, pa bo želva počakala, da uporabnik pritisne tipko.

Spremeniti moramo tole: v __init__ dodamo self.pause = 0. Želva naj ne čaka; če bomo hoteli čakanje, ga bo potrebno vključiti. Poleg tega dopišemo še metodi set_pause in no_pause, takole

def set_pause(self, s): self.pause = s def no_pause(self): self.set_pause(0)

Vse je pripravljeno, dodati je potrebno le še čakanje samo. Tu se bomo znašli: čakanje bomo dodali kar v update, h kateremu dodamo

if self.pause != 0: self.wait(self.pause) Zadoščalo bi - in poslej bomo brez opozorila delali tako, tudi if self.pause: self.wait(self.pause) Število 0 je neresnično, torej bo if self.pause resničen ravno takrat, kot je self.pause različen od 0.

Varstvo osebnih podatkov želve

Med pravila lepega vedenja pri programiranju objektov (točneje, razredov) sodi tudi skrivanje podatkov ali, v Pythonu, ki je bolj liberalen jezik, "spoštovanje zasebnosti". Vzemimo želvo Ano.

ana = turtle.Turtle() Če hočemo izvedeti, kje je Ana, lahko napišemo, recimo print(ana.x, ana.y) Tudi prestavimo jo lahko kar ročno. ana.x, ana.y = 100, 200 Vendar se to ne šteje za lepo. Do spremenljivk, ki so spravljene v objektu, naj bi dostopali le preko metod. Zato v razred Turtle dodamo funkcije, kot so def get_x(self): return self.x def get_y(self): return self.y def get_angle(self): return self.angle ... in tako naprej. Tako lahko izpišemo položaj želve z print(ana.get_x(), ana.get_y())

Za tole sicer obstaja boljši mehanizem, vendar se o njem pri Programiranju 1 ne bomo učili. Tisti, ki bi radi znali, bodo pogledali dekorator property.

Še bolj pomembno kot to, da ne škilimo v želvine osebne podatke, je, da za prestavljanje uporabljamo metode, kot je fly. Razlogi za tole so filozofsko-načelno-praktične narave. Kot prvo, kaka prihodnja verzija želve bo morda shranjevala koordinate na kak drug način. S tem, ko omogočimo dostop do podatkov le prek funkcij, moramo za zagotavljanje združljivosti poskrbeti le, da imajo funkcije enaka imena, kar se dogaja znotraj želve, pa lahko poljubno spreminjamo.

Drugi: želva je objekt ter mora vedeti in nadzorovati, kaj se dogaja z njo, ne pa, da drugi od zunaj počno z njo, kar hočejo. Ko jo, na primer, prestavimo, mora želva vedeti, da smo jo prestavili, tako da se lahko nariše na novi lokaciji. Če koordinate spreminjamo od zunaj, to ne sproži metode update.

V določenih drugih jezikih (pravzaprav najbrž kar v večini objektnih jezikov) lahko celo naročite, naj bodo določeni podatki skriti "outsiderjem". To se šteje za zelo dobro prakso in to velja početi. V drugem semestru se boste učili Javo in gotovo izvedeli veliko o tem. Tudi v Pythonu je mogoče te reči delati po pravilih; vaš predavatelj pa je en pacek. Takih stvari se mu ne ljubi početi in doslej ga še ni dovolj teplo, da bi ga izučilo. Povem vam le, da boste vedeli.

Zadnja sprememba: sobota, 20. december 2014, 18.11
◄ Testi
Modul zelva ►