Pajkov četverec in muha (26.nov. - 8.dec.)
Muha se je ujela v pajčevino. "Ah, ah," tako je vzdihovala, ko se ni mogla nikakor več rešiti, "da nisem videla teh nitk, te mreže. Ah, zakaj ne predejo pajki debelejših mrež; potem bi se gotovo ne ujela." "Tudi jaz mislim, da bi se ne," je dejal nato pajek zaničljivo in zagrabil ubogo muho, "toda mi pajki nismo tako neumni. Kdor hoče koga zapeljati in ujeti, mora nastavljati tanke, malovidne mreže, le zapomni si, muha. Tebi že povem, ker te bom takoj zadavil." Rečeno, storjeno. -- Dragotin Kette
Teta kriptografija opazi, da pajkova mreža povezuje štiri enako oddaljena vozlišča na vseh šest načinov (mimogrede: zato telesu, ki nastane kot konveksna ogrinjača, matematiki rečejo četverec) in da se nahajata muha in slepi pajek v različnih vozliščih. Muha se ne more premakniti, pajek pa se premika naključno iz enega vozlišča v drugega.
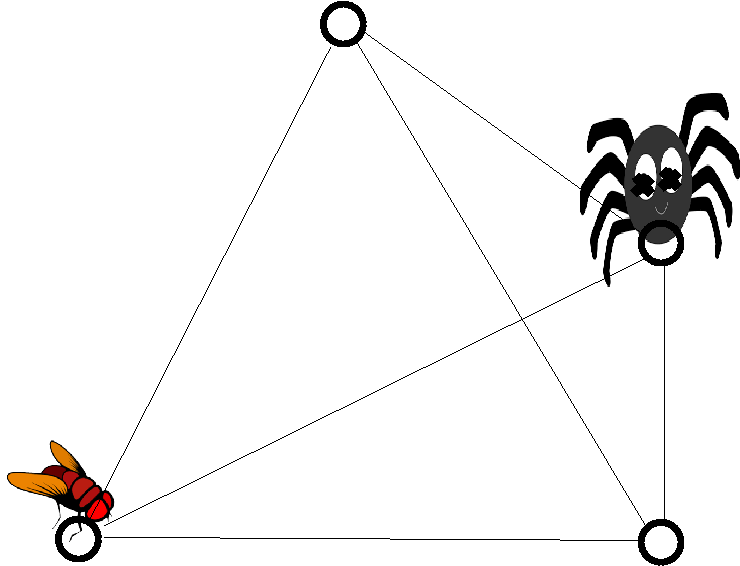
(a) Koliko je pričakovano število obratov predno pajek doseže muho?
Kaj
pa, če četverec nadomestimo z 1-skeletom kakšnega drugega Platonovega
telesa: (b) kocko, (c) oktaedrom, (d) dodekaedrom ali (e) ikozaedrom? Bodite pozorni, da je odgovor odvisen od tega, kje pajek prične svojo naključno pot.
Tedensko uganko najdete na: https://ucilnica.fri.uni-lj.si/uganka